Linear Least Squares
CPSC 406 – Computational Optimization
Overview
\[
\def\argmin{\operatorname*{argmin}}
\def\Ball{\mathbf{B}}
\def\bmat#1{\begin{bmatrix}#1\end{bmatrix}}
\def\Diag{\mathbf{Diag}}
\def\half{\tfrac12}
\def\ip#1{\langle #1 \rangle}
\def\maxim{\mathop{\hbox{\rm maximize}}}
\def\maximize#1{\displaystyle\maxim_{#1}}
\def\minim{\mathop{\hbox{\rm minimize}}}
\def\minimize#1{\displaystyle\minim_{#1}}
\def\norm#1{\|#1\|}
\def\Null{{\mathbf{null}}}
\def\proj{\mathbf{proj}}
\def\R{\mathbb R}
\def\Rn{\R^n}
\def\rank{\mathbf{rank}}
\def\range{{\mathbf{range}}}
\def\span{{\mathbf{span}}}
\def\st{\hbox{\rm subject to}}
\def\T{^\intercal}
\def\textt#1{\quad\text{#1}\quad}
\def\trace{\mathbf{trace}}
\]
- Least-quares for data fitting
- Solution properties
- Solution methods
Fitting a line to data
- Given data points \((z_i, y_i)\), \(i=1,\ldots,m\)
- Find a line \(y= c + s z\) that best fits the data
![]()
\[
\min_{c,s}\ \sum_{i=1}^m (y_i - \bar{y}_i)^2 \quad\text{st}\quad \bar y_i = c + s z_i
\]
Example: Polynomial data fitting
Given \(m\) measurements \(y_i\) taken at times \(t_i\): \[
(t_1,y_1),\ldots,(t_m,y_m)
\]
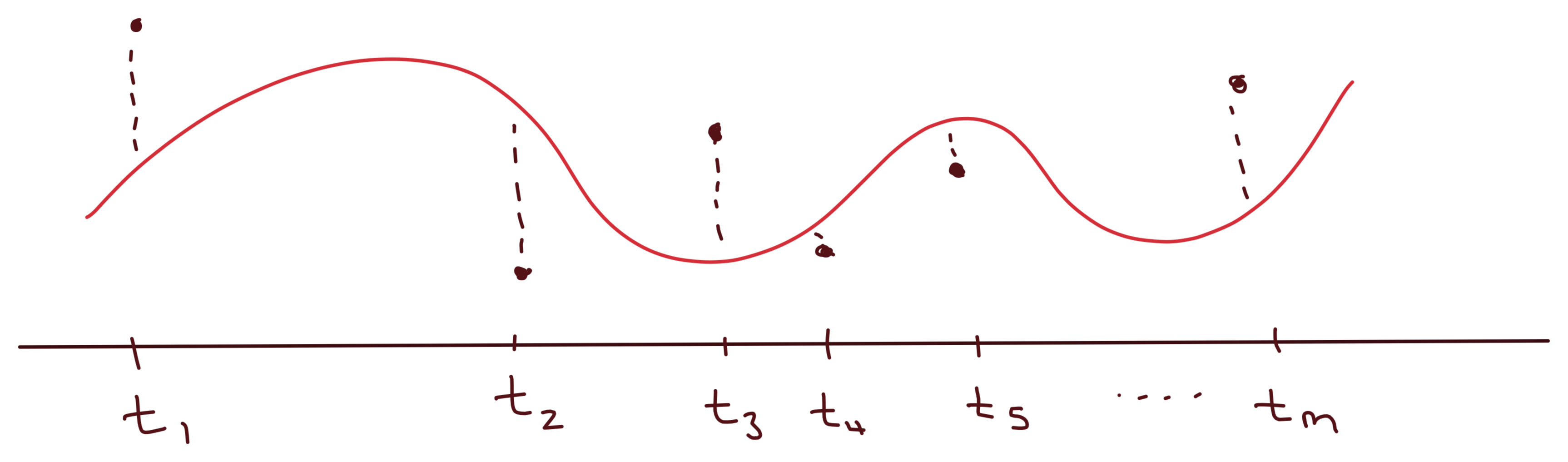
Polynomial model \(p(t)\) of degree \((n-1)\):
\[p(t) = x_0+x_1t+x_2t^2+\cdots+x_{n-1}t^{n-1} \quad (x_i=\text{coeff's})\]
Find coefficients \(x_0,x_1,\ldots,x_{n-1}\) such that
\[\begin{align}
p(t_1) &\approx y_1
\\\vdots
\\p(t_m) &\approx y_m
\end{align}\]
\[
\underbrace{
\begin{bmatrix}
1 & t_1 & t_1^2 & \cdots & t_1^{n-1}
\\\vdots & \vdots & \vdots & \ddots & \vdots
\\\ 1 & t_m & t_m^2 & \cdots & t_m^{n-1}
\end{bmatrix}}_{A}
\underbrace{
\begin{bmatrix}
x_0 \\\vdots \\\ x_{n-1}
\end{bmatrix}
}_{x}
\approx
\underbrace{
\begin{bmatrix}
y_1 \\\vdots \\\ y_m
\end{bmatrix}
}_{b}
\]
Solving linear systems
Find \(x\) where \(Ax\approx b\)
![]()
- \(m>n\) (overdetermined): possibly no exact solution
- \(m<n\) (underdetermined): possibly infinitely many solutions
- \(m=n\) (square): possibly unique solution
🎱 Question
Suppose that \(A\) is an \(m\times n\) full-rank matrix with \(m>n\). Then
- \(Ax=b\) has a unique solution for every \(b\in\mathbb{R}^m\)
- \(Ax=b\) has a solution only if \(b\in\range(A)\)
- \(Ax=b\) has a solution only if \(b\in\range(A^T)\)
- \(A\) is invertible
Over and underdetermined systems
Find \(x\) where \(Ax=b\)
- 1 solution
- overdetermined
- feasible
- \(b\in\range(A)\)
- infinitely many solutions
- underdetermined
- feasible
- \(b\in\range(A)\)
- no solution
- overdetermined
- infeasible
- \(b\not\in\range(A)\)
Least-squares optimality
\[x^*=\argmin_x f(x):=\half\|Ax-b\|_2^2=\half\sum_{i=1}^m(a_i^T x - b_i)^2\]
quadratic objective \[
\|r\|_2^2=r^Tr
\quad\Longrightarrow\quad
f(x) = \half(Ax-b)^T(Ax-b) = \half x^T A^T Ax - b^T Ax + \half b^T b
\]
gradient: \(\nabla f(x) = A^TAx-A^Tb\)
the solution of LS must be a stationary point of \(f\): \[
\nabla f(x^*) = 0
\quad\Longleftrightarrow\quad
A^TAx^*-A^Tb=0
\quad\Longleftrightarrow\quad
\underbrace{A^TAx^*=A^Tb}_{\text{normal equations}}
\]
If \(A\) has full column rank \(\quad\Longrightarrow\quad\) \(x^*=(A^TA)^{-1}A^Tb\quad(unique)\)
Geometric view
\[ A = [a_1\ a_2\ \cdots\ a_n] \quad\text{where}\quad a_i\in\mathbb{R}^m \]
![]()
\[\begin{align}
\range(A)&=\{y\mid y=Ax \text{ for some }\quad x\in\mathbb{R}^n\}
\\ \Null(A^T)&=\{z\mid A^Tz=0\}
\\ \range(A)^\perp&=\Null(A^T)
\end{align}\]
Orthogonal projection
orthogonality of residual \(r=b-Ax\) and columns of \(A\) \[
\left.
\begin{align}
a_1^T r &= 0
\\ a_2^T r &= 0
\\ \vdots
\\ a_n^T r &= 0
\end{align}
\right\}
\quad\Longleftrightarrow\quad
\begin{bmatrix}
a_1^T \\ a_2^T \\ \vdots \\ a_n^T
\end{bmatrix}r
\quad\Longleftrightarrow\quad
A^T r = 0
\quad\Longleftrightarrow\quad
r\in\Null(A^T)
\]
the following conditions are equivalent
- \(A^T r = 0\) or \(r\in\Null(A^T)\)
- \(A^TAx=A^Tb\)
projection \(y^*=Ax^* = \proj_{\range(A)}(b)\) is unique
Single regressor
\[
A = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix}
\quad\text{and}\quad
b = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix}
\quad
(n = 1)
\]
If \(m=3\) and \(b=(1, 3, 5)\) what is \(x^*\)?
