Computational Optimization

CPSC 406

Course goals and emphasis

\[ \def\argmin{\operatorname*{argmin}} \def\Ball{\mathbf{B}} \def\bmat#1{\begin{bmatrix}#1\end{bmatrix}} \def\Diag{\mathbf{Diag}} \def\half{\tfrac12} \def\int{\mathop{\rm int}} \def\ip#1{\langle #1 \rangle} \def\maxim{\mathop{\hbox{\rm maximize}}} \def\maximize#1{\displaystyle\maxim_{#1}} \def\minim{\mathop{\hbox{\rm minimize}}} \def\minimize#1{\displaystyle\minim_{#1}} \def\norm#1{\|#1\|} \def\Null{{\mathbf{null}}} \def\proj{\mathbf{proj}} \def\R{\mathbb R} \def\Re{\mathbb R} \def\Rn{\R^n} \def\rank{\mathbf{rank}} \def\range{{\mathbf{range}}} \def\sign{{\mathbf{sign}}} \def\span{{\mathbf{span}}} \def\st{\hbox{\rm subject to}} \def\T{^\intercal} \def\textt#1{\quad\text{#1}\quad} \def\trace{\mathbf{trace}} \]

Goals

• recognize and formulate the main optimization problem classes
• understand how to apply standard algorithms for each class
• recognize if an algorithm succeeded or failed
• hands-on experience with mathematical software

Emphasis

• formulating problems
• algorithms
• mathematical software

Prerequisites

Required courses

• CPSC 302 (NUmerical Computation for Algebraic Problems)
• CPSC 303 (Numerical Computation for Discretization)
• MATH 307 (Applied Linear Algebra)

Assumed background

• linear algebra – linear systems, factorizations, eigenvalues
• multivariate calculus – gradients, Hessians, Taylor series
• numerical software – eg, Julia, Matlab, Python (numpy, scipy), R

Book

Main text, available online via UBC library:

• Introduction to Nonlinear Optimization: Theory, Algorithms, and Applications with MATLAB and Python by Amir Beck, Second Edition (Springer, 2023)

Supplementary text, available online:

• Algorithms for Optimization by Mykel J. Kochenderfer and Tim A. Wheeler (MIT Press, 2019)

Role of optimization

• fitting a statistical model to data (machine learning)
• logistics, economics, finance, risk management
• theory of games and competition
• theory of computer science and algorithms
• geometry and analysis

Competing objectives

maximize

• profit
• utility
• accuracy

minimize

• cost
• risk
• error

constraints

• budget
• capacity
• physics
• fairness
• safety
• stability
• …

Isoperimetric Problem

Queen Dido’s Problem, after the founder of Carthage (814 BC)

• on then plane, length \(L\) of closed curve and enclosed area \(A\) related by \[L^2\ge 4\pi A\]

• two points of view: a circle

  • maximizes area for a given length
  • minimizes length for a given area

• same solution, but two different formulations!

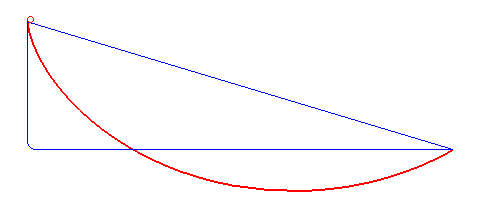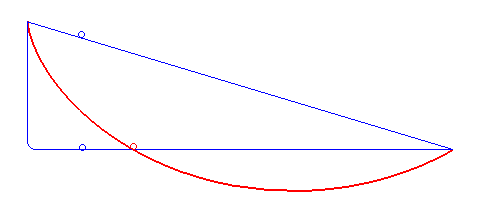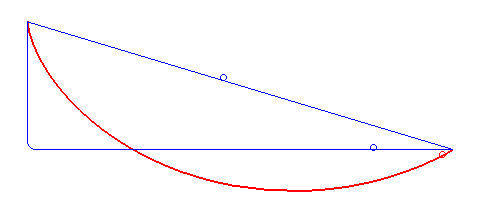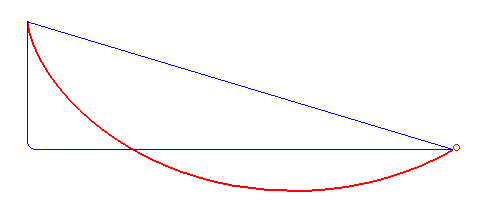
Brachistochrone problem

Find the curve of least time between two points under gravity:

• objective: time for a bead to slide from point \(A\) to point \(B\) under gravity
• constraints: bead starts at reast at \(A\) and hugs curve
• posed by Johann Bernoulli (1696) (solved by brother Jacob Bernoulli)
• solution is a cycloid: the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line

Least squares

• due to Gauss and Legendre (early 1800s)
• observations at times \(t_1,\ldots,t_m\): \[ b = (b_1,b_2,\ldots,b_m)\]
• model has parameters \(x=(x_1,x_2,\ldots,x_n)\), eg, \[m(x,t_i) = x_1 + x_2 t_i + \cdots + x_n t_i^{n-1}\]
• model may be nonlinear in parameters \(x\)
• objective is to minimize squared errors \[f(x)=\sum_i[m(x,t_i)-b_i]^2\]

Learning models

model is a simplified abstraction of process

• model parameters \[x=(x_1,x_2,…,x_n)\in\mathcal{P}\]
• prediction \[m(x)\in\mathcal{F}\]

least-error principle

• optimal parameters \(x^*\) minimizes a distance between the model and the observation
• distance is a loss function \(L:\mathcal{F}\times\mathcal{F}\toℝ\)

Mathematical Optimization

• objective function: \[f:ℝ^n\toℝ\]
• feasible set (eg, “constraints”): \[\mathcal{C}⊆ℝ^n\]
• decision variables: \[x=(x_1,x_2,\ldots,x_n)\in\mathcal{C}\]
• optimal solution \(x^*\) has smallest (or largest) value of \(f\) among all feasible points, ie, \[ f(x^*) \le f(x) \qquad \forall x\in\mathcal{C} \]

Abstract problem

• find \(x\in\mathcal{C}\) such that \(f(x)\) is minimal, eg, \[ p^* = \min_{x\in\mathcal{C}}\ f(x) \]
• optimal solution set \[\mathcal{S}:=\{x\in\mathcal{C}\mid p^*=f(x)\}\]

Varieties of optimization

• continuous vs discrete
• linear vs nonlinear
• convex vs nonconvex
• smooth vs nonsmooth
• deterministic vs stochastic
• global vs local

Steepest descent

• follow the gradient towards a minimizer
• measures the objective’s sensitivity to feasible perturbations
• usually sufficient to devise tractable and implementable algorithms

Wikipedia – Gradients and Gradient Descent in 2D

Linear programming (LP)

Applications

• resource allocation
• production planning
• scheduling
• network flows
• optimal transport

History

• Kantorovich (1912-1986) and Koopmans (1910-1985) 1975 Nobel Prize in Economics: optimal allocation of resources
• Dantzig (1914-2005) — simplex method (1947)
• von Neumann (1903-1957) and Morgenstern (1902-1977) – theory of games (1944)

Example: Scheduling

Minimize the number of hospital nurses needed to meet weekly staffing demands

Constraints

1. each nurse works 5 straight days with 2 days off
2. \(d_j\) nurses required on nights \(j=1,\ldots,7\)

First attempt

• decision variables: \(y_j\) nurses work on night \(j\)
• optimization formulation:

\[\min \Set{\sum_j y_j \ |\ y_j\ge d_j, \ j=1,\ldots,7}\]

• ❌ doesn’t respect first constraint

Scheduling: second attempt

• let \(x_j\) be number of nurses starting their 5-day shift on day \(j\):

• optimization formulation minimizes total nurses starting their shifts \[ \begin{array}{ll} \min & x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} \\ \text{st} & \begin{aligned}[t] x_{1}\phantom{+x_2+x_3 }\ \ +x_{4}+x_{5}+x_{6}+x_{7}&\ge d_{1} \\x_{1}+x_{2}\phantom{+x_{3}+x_{4}}\ \ +x_{5}+x_{6}+x_{7}&\ge d_{2} \\x_{1}+x_{2}+x_{3}\phantom{+x_{4}+x_{5}}\ \ +x_{6}+x_{7}&\ge d_{3} \\x_{1}+x_{2}+x_{3}+x_{4}\phantom{+x_{5}+x_{6}}\ \ +x_{7}&\ge d_{4} \\x_{1}+x_{2}+x_{3}+x_{4}+x_{5}\phantom{+x_{6}+x_{7}}\ \ &\ge d_{5} \\\phantom{x_{1}+}x_{2}+x_{3}+x_{4}+x_{5}+x_{6}\phantom{+x_{7}}\ \ &\ge d_{6} \\\phantom{x_{1}+x_{2}+}x_{3}+x_{4}+x_{5}+x_{6}+x_{7}&\ge d_{7} \\x_1,\ldots,x_7&\ge0 \end{aligned} \end{array} \]

• note the constraint structure. This is almost always true of practical LPs

• we may want to restrict \(x_{j}\) to be integer. That’s a much harder problem!

Quadratic programming (QP)

• generalizes linear programming
• includes
  • least-squares over linear and bound constraints (convex case; polynomial-time)
  • integer optimization (nonconvex case; NP-hard)

Applications

• portfolio optimization (1952 by Markovitz; awarded Economics Nobel in 1990)
• optimal control
• machine learning (eg, support-vector machine)

What is and why Julia?

println("Hello, world! 1 + 2 = $(1+2)")

Hello, world! 1 + 2 = 3

@code_llvm(1+2)

; Function Signature: +(Int64, Int64)
;  @ int.jl:87 within `+`
define i64 @"julia_+_11517"(i64 signext %"x::Int64", i64 signext %"y::Int64") #0 {
top:
  %0 = add i64 %"y::Int64", %"x::Int64"
  ret i64 %0
}

using Plots
plot(sin, x->sin(2x), 
     0, 2π, 
     legend=false, fill=(0,:lavender),
     size=(600,250))

sum_sqs(y) = mapreduce(x->x^2, +, y)
sum_sqs(1:3)

14

Why Julia?

• Programming language designed for scientific and technical computing
• Aims to solve the “two language problem”
• good package manager and documentation
• faster than most dynamically-typed languages, eg, Python, Matlab, R
• easier to use than most statically-typed languages, eg, C, C++, Fortran
• lots of tutorials available
• good IDE support, eg, VSCode, Jupyter, Pluto
• UBC hosts a free JupyterHub server for students (CWL required)

Optimization modeling languages

Julias has two popular optimization modeling packages:

• JuMP (Julia for Mathematical Programming)
• Convex.jl (Julia for Disciplined Convex Programming)

\[\min_{x\ge0,y\ge0}\ (1-x)^2 + 100(y-x^2)^2\]

using JuMP, Ipopt
model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, x>=0)
@variable(model, y>=0)
@objective(model, Min, (1 - x)^2 + 100 * (y - x^2)^2)
optimize!(model)
solution_summary(model)

* Solver : Ipopt

* Status
  Result count       : 1
  Termination status : LOCALLY_SOLVED
  Message from the solver:
  "Solve_Succeeded"

* Candidate solution (result #1)
  Primal status      : FEASIBLE_POINT
  Dual status        : FEASIBLE_POINT
  Objective value    : 2.44348e-21
  Dual objective value : 0.00000e+00

* Work counters
  Solve time (sec)   : 2.38895e-03
  Barrier iterations : 16

Got Clicker?

• See the iClicker Student Guide

Who is the Premier of British Columbia?

1. John Horgan
2. Andrew Wilkinson
3. David Eby
4. Justin Trudeau
5. David Suzuki

I took these courses…

1. CPSC 302 (Numerical Computation for Algebraic Problems)
2. CPSC 303 (Numerical Computation for Discretization)
3. MATH 223 (Linear Algebra)
4. MATH 307 (Applied Linear Algebra)
5. None of the above

Coursework and evaluation

• 8 homework assignments (30%)
  • programming and mathematical deriviations
  • typeset submissions, correctness, and writing quality graded
• midterm exam (30%): ✏️️ and 🗞️, short mathematical problems
• final exam (40%): multiple choice

Homework

• work alone 🏃 or in pairs 👯
• 4 late days allowed (no permission required)
  • but no more than 2 late days for a particular assignment
• submit your HW solutions to Canvas
• no solutions posted online — visit us in office hours
• typeset solutions using Jupyter or Pluto or LaTeX
  • I use Quarto for my notes

Homework 1

• no late days, no collaborators
• should feel familiar
• due next week

Resources

• see the course home page for schedule
• visit Canvas for links to
  • Canvas for discussions and announcements
  • Canvas for homework submission
• TA and instructor office hours start week 2