Convex Sets

CPSC 406 – Computational Optimization

Convex sets

\[ \def\argmin{\operatorname*{argmin}} \def\argmax{\operatorname*{argmax}} \def\bbar{\bar b} \def\Ball{\mathbf{B}} \def\bmat#1{\begin{bmatrix}#1\end{bmatrix}} \def\Diag{\mathbf{Diag}} \def\half{\tfrac12} \def\int{\mathop{\rm int}} \def\ip#1{\langle #1 \rangle} \def\maxim{\mathop{\hbox{maximize}}} \def\maximize#1{\displaystyle\maxim_{#1}} \def\minim{\mathop{\hbox{minimize}}} \def\minimize#1{\displaystyle\minim_{#1}} \def\norm#1{\|#1\|} \def\Null{{\mathbf{null}}} \def\Bscr{\mathcal{B}} \def\Nscr{\mathcal{N}} \def\Pscr{\mathcal{P}} \def\proj{\mathbf{proj}} \def\R{\mathbb R} \def\Re{\mathbb R} \def\Real{\mathbb R} \def\Rn{\R^n} \def\rank{\mathbf{rank}} \def\range{{\mathbf{range}}} \def\sign{{\mathbf{sign}}} \def\span{{\mathbf{span}}} \def\st{\hbox{subject to}} \def\T{^\intercal} \def\textt#1{\quad\text{#1}\quad} \def\trace{\mathbf{trace}} \def\xbar{\bar x} \def\pstar{p^*} \def\xstar{x^*} \def\xhat{\hat x} \]

• definition
• subspaces, affine sets, and spans
• halfspaces and hyperplanes
• cones and hulls
• operations that preserve convexity

Lines and line segments

• line through two points \(x_1,x_2\in\Rn\) is the set

\[ \set{z \mid z = \theta x_1 + (1-\theta)x_2,\ \theta\in\R} \]

• \(x\in\Rn\) is a convex combination of vectors \(x_1,\ldots,x_k\) if \[ x = \sum_{i=1}^k \theta_i x_i, \quad \sum_{i=1}^k \theta_i = 1, \quad \theta_i \ge 0 \]

Convex sets and hulls

• the convex hull of a set of points \(\mathcal{S}\) contains all convex combinations of points in \(\mathcal{S}\): \[ \text{conv}(\mathcal{S}) = \left\{ \sum_{i=1}^k \theta_i x_i \mid x_i\in\mathcal{S},\ \sum_{i=1}^k \theta_i = 1, \ \theta_i\ge 0 \right\} \]

 

 

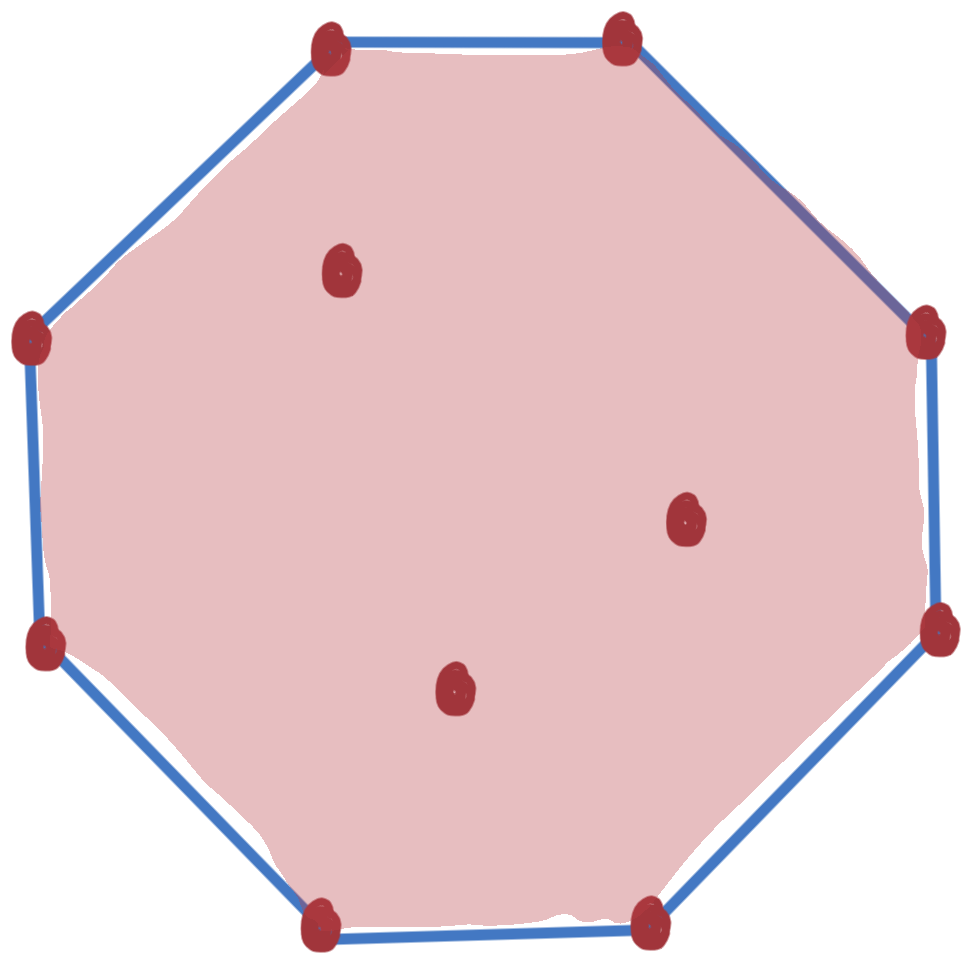
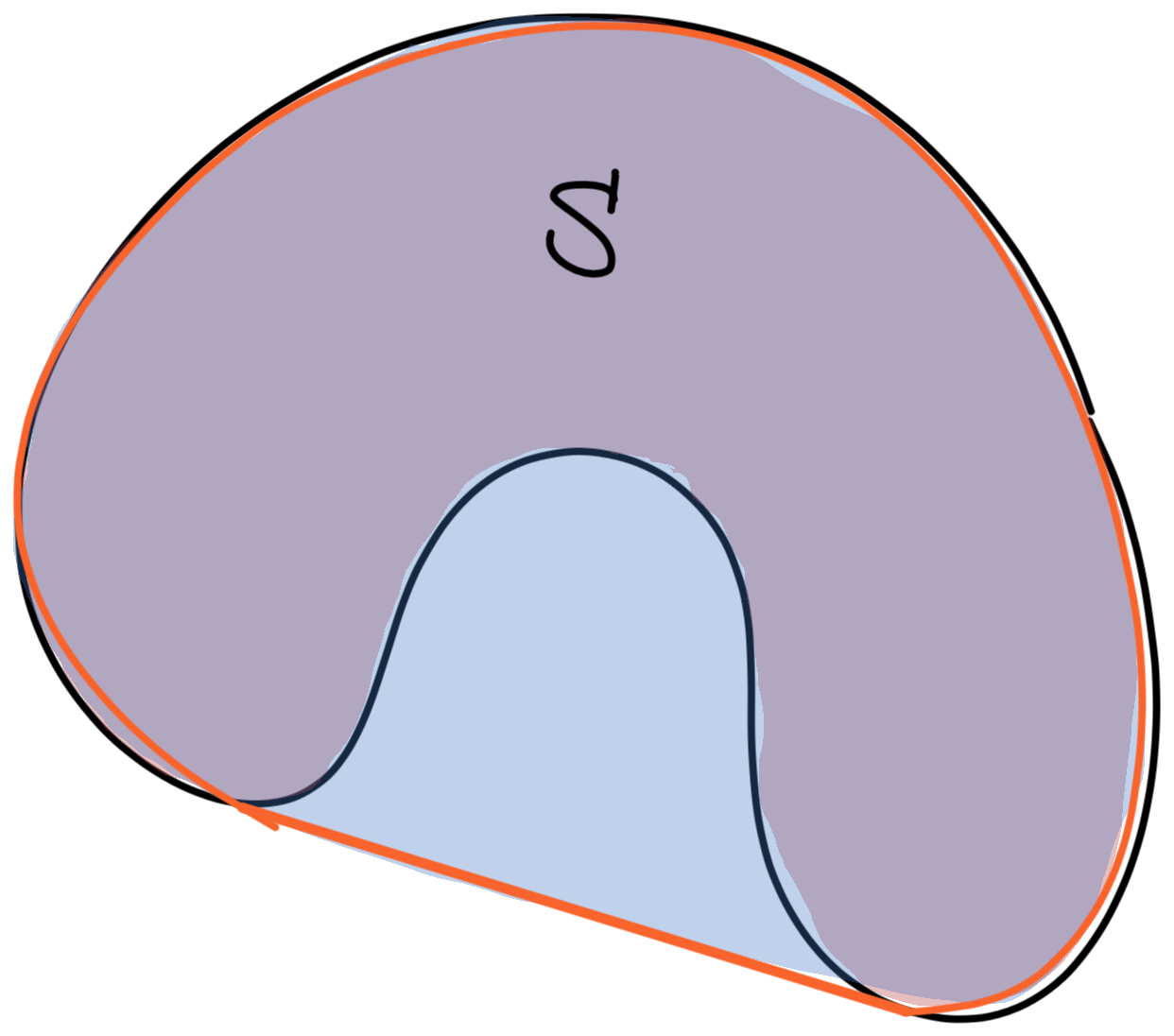
• \(\mathcal{C}\subset\Rn\) is convex if it contains all convex combinations of its elements, ie, \(\mathcal{C}= \text{conv}(\mathcal{C})\)

 

 

Question

Show that the norm ball \[\mathbb{B} = \{x \in \mathbb{R}^n \mid \|x - x_c\| \leq r\}\] is a convex set.

Hint: use the triangle inequality

Subspaces, spans, and affine sets

• \(\mathcal{S}\subset\Rn\) is a subspace if it contains all linear combinations of points in the set, ie,

\[ \alpha x + \beta y \in \mathcal{S}, \ \forall x,y\in\mathcal{S}, \ \forall \alpha,\beta\in\R \]

• for any \(m\times n\) matrix \(A\), its range and nullspace are subspaces of \(\Rn\): \[ \mathop{\bf range}(A) = \{Ax \mid x\in\Rn\} \quad\text{and}\quad \mathop{\bf null}(A^T) = \{z \mid A^Tz = 0\} \]

• the span of a collection of vectors \({x_1,\ldots,x_k}\) is the subspace of all vectors

\[ \mathop{\bf span}(x_1,\ldots,x_n) = \left\{\sum_{i=1}^k \theta_i x_i, \quad \forall\theta_i\in\R \right\} \]

• an affine set is a translated a subspace, ie, for fixed \(x_0\in\Rn\) and subspace \(\mathcal{S}\),

\[ \mathcal{L} = \{x_0 + v \mid v\in\mathcal{S}\} \equiv x_0 + \mathcal{S} \]

• \(\mathcal{S}\) is the subspace parallel to \(\mathcal{L}\)

Halfspaces and hyperplanes

fix nonzero vector \(a\in\Rn\) and scalar \(\beta\)

• hyperplanes and halfspaces, respectively, have the form

\[ \mathcal{H} = \{x \mid a^Tx = \beta\} \quad\text{and}\quad \mathcal{H}_- = \{x \mid a^Tx \le \beta\} \]

• \(a\) is the normal to the hyperplane
• hyperplanes are affine and convex
• halfspaces are convex but not affine

Question

Express the nonnegative orthant \[ \Rn_+ = \{x \mid x_i \ge 0, \ i=1,\ldots,n\} \] as an intersection of \(n\) halfspaces.

Convex polyhdra

\(\mathcal{S}\) is a convex polyhdron if it’s the intersection of a finite number of halfspaces:

\[ \mathcal{S} = \bigcap_{i=1}^m\{x \mid a_i^Tx \le β_i\} = \set{x \mid Ax \le b} \]

where

\[ A = \begin{bmatrix} a_1^T\\\vdots\\ a_m^T \end{bmatrix} \in\R^{m\times n} \quad\text{and}\quad b\in\R^m \]

Question

Express the probability simplex \[ \Delta = \left\{x \ \middle | \ \sum_{i=1}^{n}x_i=1, \ x_i\ge 0\right\} \] as the intersection of \(n\) halfspaces and a hyperplane.

Convex cones

• a set \(\mathcal{K}\subset\Rn\) is a cone if \(x\in\mathcal{K} \ \Longleftrightarrow \ \alpha x\in\mathcal{K}\) for all \(\alpha\ge 0\)

• a convex cone is a cone that is also convex

\[ x, y \in \mathcal{K} \text{ and } \ \alpha, \beta\ge 0 \ \implies \ \alpha x + \beta y \in \mathcal{K} \]

Examples

\[ \begin{aligned} \Rn_+ &= \{x \mid x_i \ge 0, \ i=1,\ldots,n\} &\quad\text{(nonnegative orthant)}\\[10pt] \mathcal{L}_+^n&=\left\{\begin{bmatrix}x\\t\end{bmatrix}\in\R^{n+1} \, \middle |\, \|x\|_2\le t, \ x\in\Rn, \ t\in\R\right\} &\quad\text{(second-order cone)}\\[10pt] \mathcal{S}_+^n&=\Set{X\in\R^{n\times n} \mid X\succeq 0} &\quad\text{(positive semidefinite cone)} \end{aligned} \]

Application: Robust Portfolio Optimization

Objective: Balance risk and return by optimizing asset allocation weights \(w\) in a portfolio: \[ \max_{w} \quad \mu^T w \quad \text{subject to} \quad w^T \Sigma w \le \sigma^2, \quad \mathbf{1}^T w = 1 \] where \(\mu\) is the vector of expected returns and \(\Sigma\) is the covariance matrix and \(\sigma^2\) is the maximum acceptable risk.

• Transform the quadratic risk constraint into a second-order cone constraint: \[ \|\Sigma^{1/2} w\|_2 \le \sigma. \]
• Optimization Problem:
  \[ \begin{aligned} \max_{w} \quad & \mu^T w \\ \text{s.t.} \quad & \|\Sigma^{1/2} w\|_2 \le \sigma, \\ & \mathbf{1}^T w = 1. \end{aligned} \]
• This formulation is a second-order cone program (SOCP) that directly maximizes return while keeping risk below a specified threshold.

Operations that preserve convexity

Let \(\mathcal{C}_1,\mathcal{C}_2\) be convex sets in \(\Rn\).

• nonnegative scaling:

\[ \theta\mathcal{C}_1 = \{\theta x \mid x\in\mathcal{C}_1\}, \quad \theta\ge 0 \]

• intersection:

\[ \mathcal{C}_1\cap\mathcal{C}_2 \]

• sum:

\[ \mathcal{C}_1+\mathcal{C}_2 = \{x+y \mid x\in\mathcal{C}_1,\ y\in\mathcal{C}_2\} \]