Gradients,
Linearizations,
and Optimality

CPSC 406 – Computational Optimization

Gradients, linearizations, and optimality

directional derivatives
gradients
first-order expansions
necessary conditions for optimality

Optimality

\[ \min_x\, f(x) \quad\text{where}\quad f:\Rn\to\R \]

$x^*\in\Rn$ is a

global minimizer if $f(x^*)\leq f(x)$ for all $x$
strict global minimizer if $f(x^*)< f(x)$ for all $x$
local minimizer if $f(x^*)\leq f(x)$ for all $x\in\epsilon\Ball(x^*)$
strict local minimizer if $f(x^*)< f(x)$ for all $x\in\epsilon\Ball(x^*)$

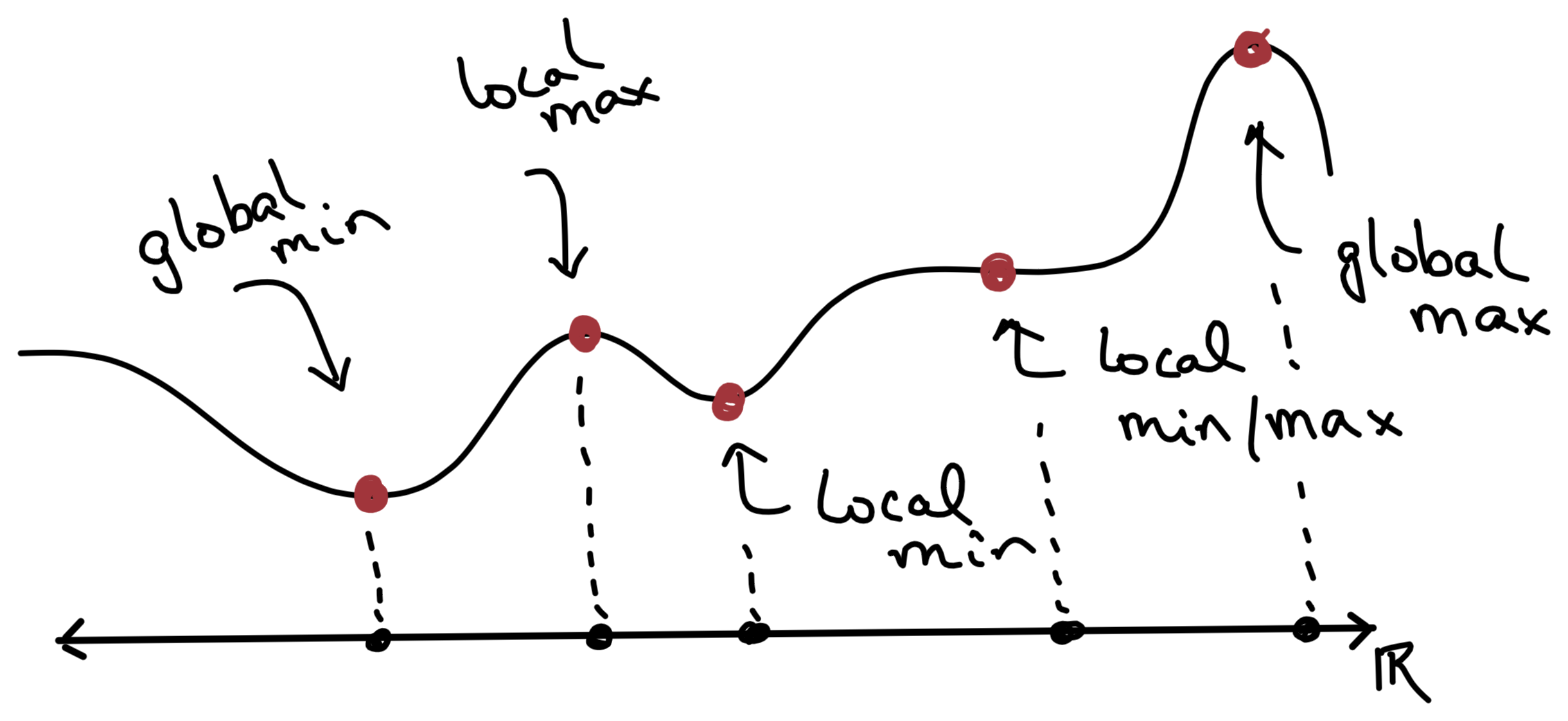
Maximizers

flip inequalities for analogous maximizer def’s
$\displaystyle\argmin_x \{f(x)\}=\argmax_x \{-f(x)\}$

Optimal attainment

an optimal value may not be attained, eg,
- $\displaystyle\inf_x\, e^{-x}$ is not attained for any $x\in\R$
an optimal value may not exist, eg,
- $\displaystyle\min_x\, -x^2$ has no minimizer (unbounded below)
global solution set (may be empty / unique element / many elements)

\[\argmin_x f(x) = \{\bar x\mid f(\bar x) \le f(x) \text{ for all } x\}\]
optimal values are unique even if an optimal point is not unique

Theorem 1 (Coercivity implies existence of minimizer) If $f:\Rn\to\R$ is continuous and $\lim_{\|x\|\to\infty}f(x)=\infty$ (coercive), then $\min_x\, f(x)$ has a global minimizer.

Example

\[ \min_{x\in\R^2}\, \frac{x_1+x_2}{x_1^2+x_2^2+1} \]

global minimizer at $-\frac{1}{\sqrt 2}(1,1)$
global maximizer at $\phantom-\frac{1}{\sqrt 2}(1,1)$

scalar variable ($n$)

Local optimality (1-D)

Let $f:\R\to\R$ be differentiable. The point $x=x^*$ is a

local minimizer if \[ \underbrace{f'(x) = 0}_{\text{stationary at $x$}} \textt{and} \underbrace{f''(x) > 0}_{\text{(strictly) convex at $x$}} \]
local maximizer if \[ \underbrace{f'(x) = 0}_{\text{stationary at $x$}} \textt{and} \underbrace{f''(x) < 0}_{\text{(strictly) concave at $x$}} \]
if $f'(x)=0$ and $f''(x)=0$, not enough information, eg,
- $f(\bar x)=x^3$ $\quad\Longrightarrow\quad$ $x=0$ in not a local minimizer or maximizer even though $f'(0)=0$
- $f(\bar x)=x^4$ $\quad\Longrightarrow\quad$ $x=0$ is the unique global minimizer even though $f''(0)=0$

Local optimality (1-D): motivation

suppose $f'(x^*)=0$ and $f''(x^*)>0$ at some $x^*$
Taylor series, where remainder term $\omicron(\alpha)/\alpha\to0$ as $\alpha\to0^+$:

\[ f(x^*+\Delta x) = f(x^*) + \underbrace{f'(x^*)\Delta x}_{=0} + \underbrace{\tfrac{1}{2}f''(x^*)(\Delta x)^2}_{>0} + \omicron((\Delta x)^2) \]

divide both sides by $(\Delta x)^2$; for $\Delta x$ small enough, right-hand side is positive:

\[ \frac{f(x^*+\Delta x) - f(x^*)}{(\Delta x)^2} = \tfrac{1}{2}f''(x^*)+ \frac{\omicron((\Delta x)^2)}{(\Delta x)^2} > 0 \]

implies $f(x^*+\Delta x) > f(x^*)$ for $\Delta x$ small enough

multivariable (n>1)

Directional derivative

restrict $f:\Rn\to\R$ to the ray $\{x+\alpha d\mid \alpha\in\R_+\}$:

\[ \phi(\alpha) = f(x+\alpha d) \qquad \phi'(0) = \lim_{\alpha\to 0^+}\frac{\phi(\alpha)-\phi(0)}{\alpha} \]

Definition 1 The directional derivative of $f$ at $x\in\R^n$ in the direction $d\in\R^n$ is \[ f'(x;d) = \lim_{α\to0^+}\frac{f(x+αd)-f(x)}{α}. \]

partial derivatives are directional derivatives along each canonical basis vector $e_i$: \[ \frac{\partial f}{\partial x_i}(x) = f'(x;e_i) \quad\text{with}\quad e_i(j) = \begin{cases} 1 & j=i\\ 0 & j\ne i\end{cases} \]

Descent directions

a nonzero vector $d$ is a descent direction of $f$ at $x$ if

\[ f(x+\alpha d) < f(x) \quad \forall \alpha \in (0, \epsilon) \text{ for some } \epsilon > 0 \]

equivalently, the directional derivative is negative:

\[ \begin{aligned} f'(x;d) := \lim_{\alpha\to 0^+}\frac{f(x+\alpha d)-f(x)}{\alpha} < 0 \end{aligned} \]

Gradients

if $f:\Rn\to\R$ is continuously differentiable (ie, differentiable at all $x$ and $\nabla f$ is continuous) the gradient of $f$ at $x$ is the vector

\[ \nabla f(x)= \begin{bmatrix} \frac{\partial f}{\partial x_1}(x)\\ \vdots\\ \frac{\partial f}{\partial x_n}(x) \end{bmatrix} \in \Rn \]

gradient and directional derivative related via

\[ f'(x;d) = \nabla f(x)\T d \]

direction derivative gives
- the rate of change of $f$ at $x$ in the direction $d$
- (if $\|d\|=1$) the projection of $\nabla f(x)$ onto $d$

Εxample

\[ f(x) = x_1^2 + 8x_1x_2 - 2x_3^2 % \qquad % \nabla f(x) = \begin{bmatrix} % 2x_1 + 8x_2\\ % 8x_1\\ % -4x_3 % \end{bmatrix} \]

What is $f'(x;d)$ for $x=(1, 1, 2)$ and $d=(1,0,1)$?

Automatic differentiation

\[f(x) = (1 - x_1)^2 + 100(x_2 - x_1^2)^2\]

gradient

using ForwardDiff
f(x) = (1 - x[1])^2 + 100*(x[2] - x[1]^2)^2
∇f(x) = ForwardDiff.gradient(f, x)
x = [1.0, 1.0]
@show ∇f(x);

∇f(x) = [-0.0, 0.0]

directional derivative

fp(x, d) = ForwardDiff.derivative(α->f(x + α*d), 0.)
d = [1.0, 0.0]
fp(x, d)
fp(x, d) == ∇f(x)'d

true

Visualizing the gradient

Definition 2 (Level set) The $\alpha$-level set of $f$ is the set of points $x$ where the function value is at most $\alpha$:

\[ [f\leq \alpha] = \{x\mid f(x)\leq \alpha\} \]

a direction $d$ points “into” the level set $[f\leq f(x)]$ if \[f'(x;d) := \nabla f(x)\T d < 0\]
the gradient $\nabla f(x)$ is orthogonal to the level set defined by $f(x)$

Linear approximation

if $f:\Rn\to\R$ is differentiable at $x$, then for any direction $d$

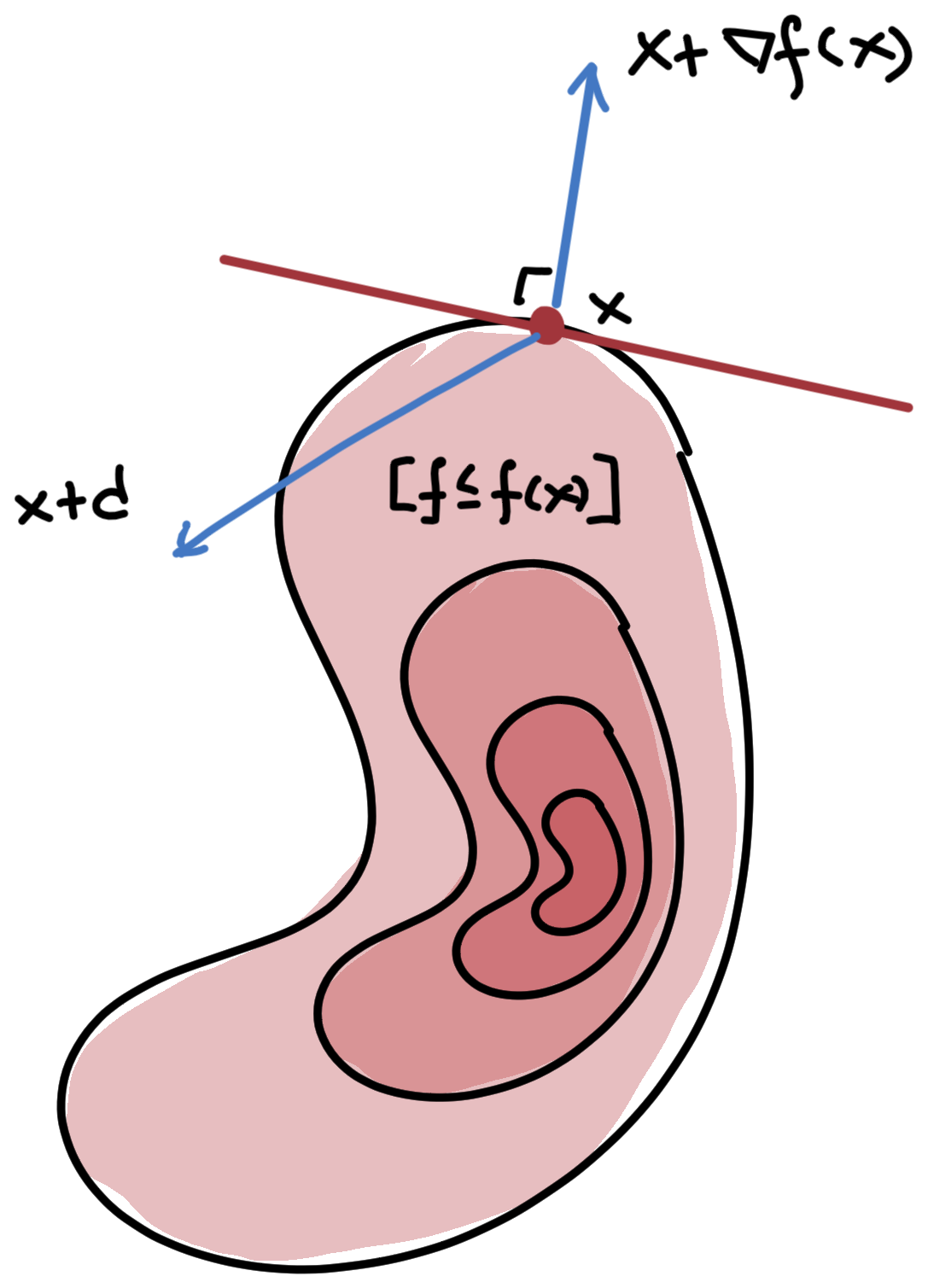
\[ \begin{aligned} f(x+d) = f(x) + \nabla f(x)\T d + \omicron(\norm{d}) = f(x) + f'(x;d) + \omicron(\norm{d}) \end{aligned} \]

the remainder $\omicron:\R_+\to\R$ decays faster than $\norm{d}$

\[\lim_{α\to0+}\frac{\omicron(α)}{α}=0\]

1st-order conditions

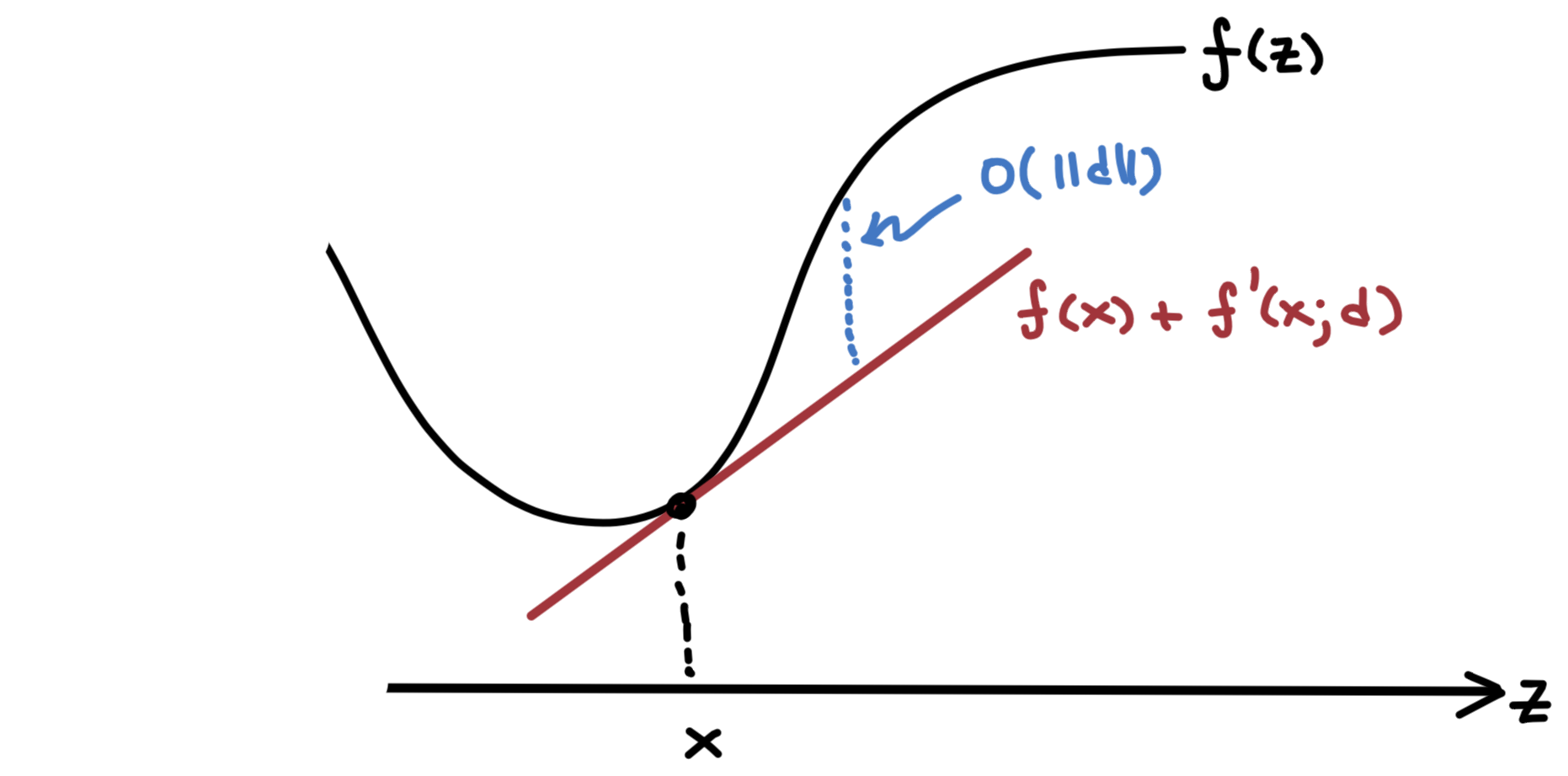
Theorem 2 (Necessary first-order conditions) For $f:\Rn\to\R$ differentiable, $x^*$ is a local minimizer only if it is a stationary point:

\[ \nabla f(x^*) = 0 \]

up to first order, for any direction $d$

\[ \begin{aligned} f(x^*+\alpha d) - f(x^*) &= \nabla f(x^*)\T (\alpha d) + o(\alpha\|d\|)\\ &= \alpha f'(x^*;d) + o(\alpha\|d\|) \end{aligned} \]

because $f$ is (locally) minimal at $x^*$

\[ \begin{aligned} 0\le\lim_{\alpha\to 0^+}\frac{f(x^*+\alpha d) - f(x^*)}{\alpha} &= f'(x^*;d)=\nabla f(x^*)\T d \end{aligned} \]

because this holds for all $d$, necessarily $\nabla f(x^*)=0$

Example: Quadratic

\[ f(x) = \tfrac{1}{2}x\T Hx - c\T x + \gamma, \quad H=H\T\in\Rn, \quad c\in\Rn \]

$x^*$ is a local minimizer only if $\nabla f(x^*)=0$, ie, \[ 0 = \nabla f(x^*) = Hx^* - c \quad\Longrightarrow\quad Hx^*=c \]
if $\Null(H)\ne\emptyset$ and $c\in\range(H)$, then there exists $x_0$ such that $Hx_0=b$ and \[ \argmin_x\, f(x) = \{\, x_0 + z \mid z\in\Null(H)\,\} \]

Example: Least squares

\[ f(x) = \tfrac{1}{2}\|Ax-b\|^2 = \tfrac{1}{2}(Ax-b)\T(Ax-b) = \tfrac{1}{2}x\T \underbrace{(A\T A)}_{=H}x - \underbrace{(b\T A)}_{=c\T}x + \underbrace{\tfrac{1}{2}b\T b}_{=\gamma} \]

$x^*$ is a least-squares solution if and only if it satisfies the normal equations \[ 0 = \nabla f(x^*) = A\T Ax^* - A\T b \quad\Longleftrightarrow\quad A\T Ax^*=A\T b \]

Example: Nonlinear least squares

\[ f(x) = \tfrac{1}{2}\|r(x)\|^2 = \tfrac{1}{2}r(x)\T r(x) = \tfrac12\sum_{i=1}^m r_i(x)^2 \] where \[ r(x) = \begin{bmatrix} r_1(x)\\ \vdots\\ r_m(x) \end{bmatrix} \quad\text{where}\quad r_i:\Rn\to\R,\ i=1,\ldots,m \]

gradient

\[ \begin{aligned} \nabla f(x) = \nabla\left[\tfrac{1}{2}\sum_{i=1}^m r_i(x)^2\right] &= \sum_{i=1}^m \nabla r_i(x) r_i(x)\\ &= \underbrace{\begin{bmatrix} \, \nabla r_1(x) \mid \cdots \mid \nabla r_m(x)\, \end{bmatrix}}_{\nabla r(x)\equiv J(x)\T} \begin{bmatrix} r_1(x)\\ \vdots\\ r_m(x) \end{bmatrix} = J(x)\T r(x) \end{aligned} \]

Gradients and convergence

using Plots
using Optim: g_norm_trace, f_trace, iterations, LBFGS, optimize

f(x) = (1 - x[1])^2 + 100 * (x[2] - x[1]^2)^2

x0 = zeros(2) 
res = optimize(f, x0, method=LBFGS(), autodiff=:forward, store_trace=true)
fval, gnrm, itns = f_trace(res), g_norm_trace(res), iterations(res)
plot(0:itns, [fval gnrm], yscale=:log10, lw=3, label=["f(x)" "||∇f(x)||"], size=(550, 350), legend=:inside)

Gradients, Linearizations, and Optimality