Regularization

CPSC 406 – Computational Optimization

Regularized least squares

  • competing objectives
  • Tikhonov regularization (ridge regression)
  • least-norm solutions

Multi-objective optimization

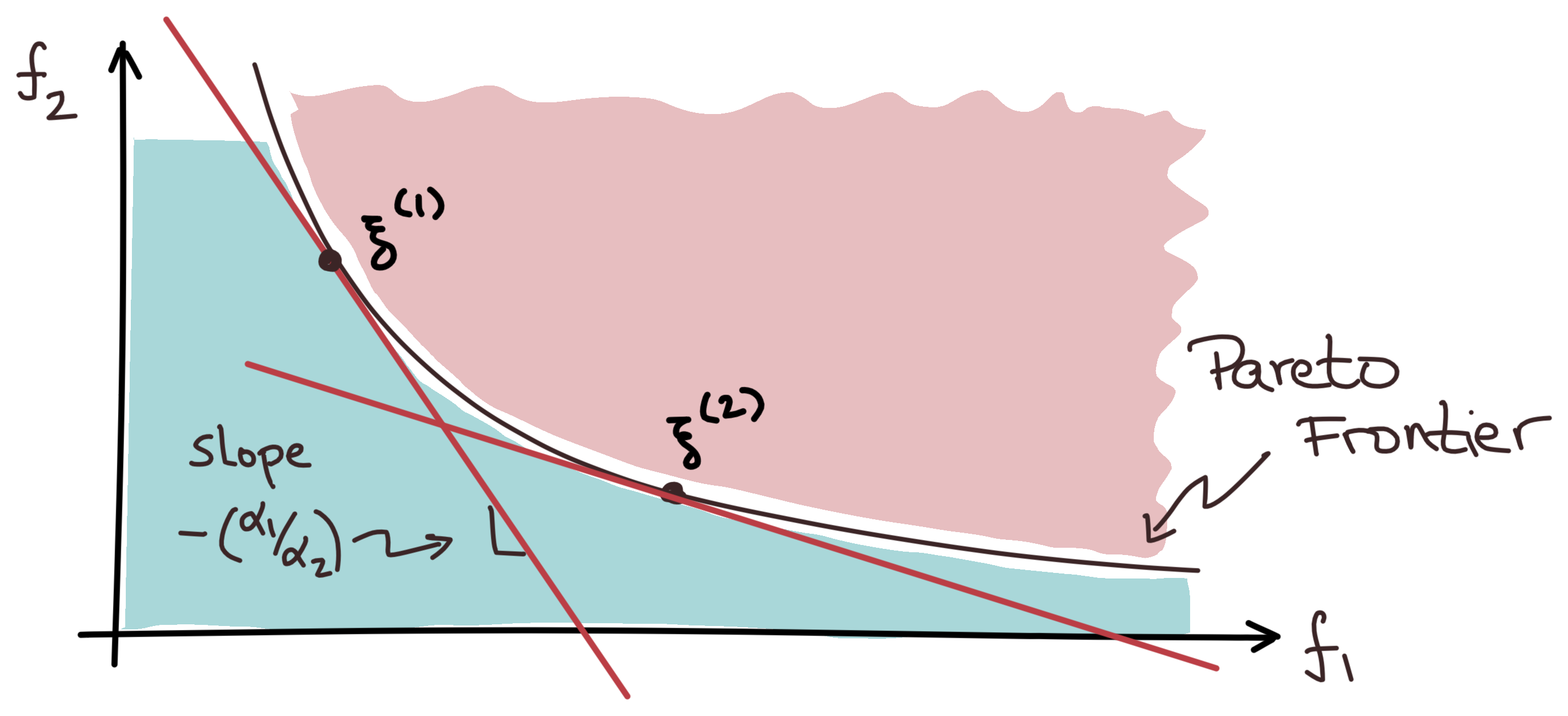
Many problems need to balance competing objectives, eg,

  • choose \(x\) to minimize \(f_1(x)\) or \(f_2(x)\)
  • can make \(f_1\) or \(f_2\) small, but not both, eg

\[ x^{*} = \argmin_x f_1(x) \quad\Longrightarrow\quad f_1(x^{*}) \leq f_2(x^{*}) \]


The Pareto frontier

\(\xi^{(i)} := \{f_1(x^{(i)}),\ f_2(x^{(i)})\}\)

  • \(\xi^{(1)}\) is not efficient
  • \(\xi^{(3)}\) dominates \(\xi^{(1)}\)
  • \(\xi^{(2)}\) is infeasible

Weighted-sum objective

Common approach is to weight the sum of objectives: \[ \min_x \ \alpha_1 f_1(x) + \alpha_2 f_2(x) \]

  • penalty parameters \(\alpha_1, \alpha_2>0\)
  • ratio \(\frac{\alpha_1}{\alpha_2}\) determines relative objective weights

\[ \argmin_x \{\, \alpha_1 f_1(x) + \alpha_2 f_2(x)\} = \argmin_x \{\, f_1(x) + \tfrac{\alpha_2}{\alpha_1} f_2(x)\} \]

Two efficient solutions on the Pareto Frontier


  • \(x^{(1)}\) solution for \(\alpha_1>\alpha_2\)
  • \(x^{(2)}\) solution for \(\alpha_2>\alpha_1\)

Nonconvex Pareto frontier

Wikipedia, courtesy G. Jacquenot, CC-BY-SA-3.0

Tikhonov regularization

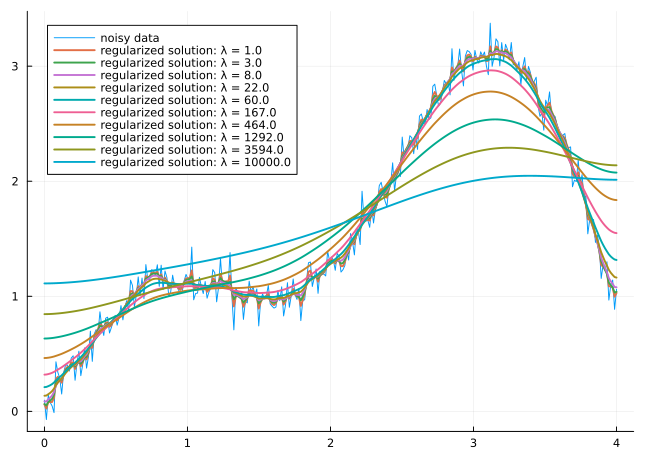
\[ \min_x\ \tfrac12\|Ax - b\|^2 + \tfrac12\lambda\|Dx\|^2 \]

  • known as ridge regression in statistics and machine learning
  • \(\|Dx\|^2\) is the regularization penalty (often \(D:=I\))
  • \(\lambda\) is the positive regularization parameter
  • equivalent expression for objective

\[ \|Ax-b\|^2 + \lambda\|Dx\|^2 = \left\|\begin{bmatrix}A\\\sqrt\lambda D\end{bmatrix}x - \begin{bmatrix}b\\0\end{bmatrix}\right\|^2 \]

  • Normal equations (unique solution if \(D\) full rank)

\[ (A\T A + \lambda D\T D)x = A\T b \]

Question

Given tall \(m\times n\) matrix \(A\) with SVD \(A = U\Sigma V^T\), where \(\Sigma\) is the diagonal matrix of singular values \(\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_{n} \ge 0.\) Let \[ M \;=\; \begin{bmatrix} A \\[2pt] \sqrt{\lambda}\,I \end{bmatrix} \] For \(i=1,\dots,n\), are the singular values of \(M\) are

  1. \(\sigma_i\)
  2. \(\sigma_i^2 + \lambda\)
  3. \(\sqrt{\sigma_i^2 + \lambda}\)
  4. \(\sigma_i + \sqrt{\lambda}\)

Hint: Recall that the singular values of \(M\) are the square roots of the eigenvalues of \(M^TM\).

Example — signal denoising

observe noisy measurements \(y\) of a signal \[ b = \hat x + \eta \textt{where} \left\{\begin{aligned} x^\natural&\in\Rn\ \text{is true signal} \\\eta &\in\R^n\ \text{is noise} \end{aligned} \right. \]

 

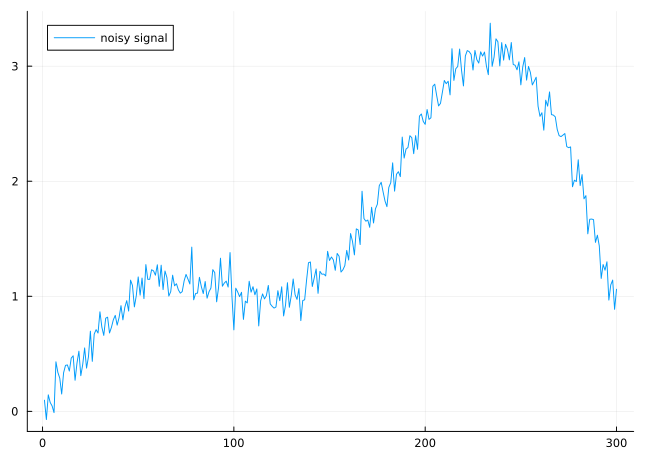
Noisy smooth signal

 

Example – least-squares formulation

  • Naive least squares fits noise perfectly: \(b\) solves \(\min_x\|x - b\|^2\)

  • assumption: \(x^\natural\) is smooth \(\quad\Longrightarrow\quad\) balance fidelity to data against smoothness

\[ \min_x\ \underbrace{\|x - b\|^2}_{f_1(x)} +\underbrace{\lambda\sum_{i=1}^{n-1}\|x_i-x_{i+1}\|^2}_{f_2(x)} \]

  • \(f_2(x)\) is penalizes jumps in signal

Example — matrix notation

  • Define the \((n-1)\times n\) finite difference matrix \[ D = \begin{bmatrix} 1 & -1 & \phantom-0 & \cdots & 0 & \phantom-0 \\0 &\phantom-1 & -1 & \cdots & 0 & \phantom-0 \\\vdots & \phantom-\vdots & \phantom-\vdots & \ddots & \vdots &\phantom-\vdots \\0 & \phantom-0 & \phantom-0 & \cdots & 1 & -1 \end{bmatrix} \quad\Longrightarrow\quad \sum_{i=1}^{n-1}\|x_i-x_{i+1}\|^2 = \|Dx\|^2 \]
  • least-squares objective \[ \|x - b\|^2 + \lambda\|Dx\|^2 = \left\|\begin{bmatrix}I\\\sqrt\gamma D\end{bmatrix}x - \begin{bmatrix}b\\0\end{bmatrix}\right\|^2 \]
  • Normal equations \[ (I + \gamma D\T D)x = b \]

Sparse matrices

\(D\) is sparse: only \(2n-2\) nonzero entries (2 per row)

using SparseArrays: spdiagm
finiteDiff(n) = spdiagm(0 => ones(n), +1 => -ones(n-1))[1:n-1,:]
finiteDiff(4)
3×4 SparseArrays.SparseMatrixCSC{Float64, Int64} with 6 stored entries:
 1.0  -1.0    ⋅     ⋅ 
  ⋅    1.0  -1.0    ⋅ 
  ⋅     ⋅    1.0  -1.0

Equivalent formulations

\[ \begin{aligned} \min_x\,&\{f_1(x) + \lambda f_2(x)\,\}\\ \min_x\,&\{f_1(x)\mid f_2(x) \leq τ\} \\ \min_x\,&\{f_2(x)\mid f_1(x) \leq \sigma\} \end{aligned} \]

Code 
# Generate a small random overdetermined system
Random.seed!(123)
m, n = 9, 3
A = randn(m, n)
b = randn(m)

# Solve min ||Ax-b||^2 + λ||x||^2
function solveTikhonov(A, b, λ)
    x = Variable(n)
    problem = minimize(sumsquares(A*x - b) + λ*sumsquares(x))
    solve!(problem, ECOS.Optimizer(), verbose=false, silent_solver=true)
    x = evaluate(x)
    return norm(A*x-b), norm(x) 
end

# Solve min ||Ax-b||^2 s.t. ||x||^2 ≤ τ
function solveConstrained(A, b, τ)
    x = Variable(n)
    problem = minimize(sumsquares(A*x - b), sumsquares(x)≤τ)
    solve!(problem, ECOS.Optimizer(), verbose=false, silent_solver=true)
    x = evaluate(x)
    return norm(A*x-b), norm(x) 
end

# Solve min ||x||^2 s.t. ||Ax-b||^2 ≤ σ
function solveFlipped(A, b, σ)
    x = Variable(n)
    p = minimize(sumsquares(x), sumsquares(A*x - b) ≤ σ)
    solve!(p, ECOS.Optimizer(), verbose=false, silent_solver=true)
    x = evaluate(x)
    return norm(A*x-b), norm(x)
end

# Plot ||x|| vs. ||Ax-b|| for various values of λ, τ, and σ
prange = LogRange(1e-2, 1e2, 50)
p1 = map(λ -> solveTikhonov(A, b, λ), prange)
p2 = map(τ -> solveConstrained(A, b, τ), prange)
p3 = map(σ -> solveFlipped(A, b, σ), range(1e-0, 1e1, 50))
p = plot(xlabel="||x||", ylabel="||Ax-b||", ticks=false)
scatter!(p, [pair[2] for pair in p1], [pair[1] for pair in p1], label="Tikhonov", mark=:circle)
scatter!(p, [pair[2] for pair in p2], [pair[1] for pair in p2], label="Constrained", mark=:square)
scatter!(p, [pair[2] for pair in p3], [pair[1] for pair in p3], label="Flipped", mark=:diamond)
Figure 1