SVD

CPSC 406 – Computational Optimization

Overview

\[ \def\argmin{\operatorname*{argmin}} \def\Ball{\mathbf{B}} \def\bmat#1{\begin{bmatrix}#1\end{bmatrix}} \def\Diag{\mathbf{Diag}} \def\half{\tfrac12} \def\int{\mathop{\rm int}} \def\ip#1{\langle #1 \rangle} \def\maxim{\mathop{\hbox{\rm maximize}}} \def\maximize#1{\displaystyle\maxim_{#1}} \def\minim{\mathop{\hbox{\rm minimize}}} \def\minimize#1{\displaystyle\minim_{#1}} \def\norm#1{\|#1\|} \def\Null{{\mathbf{null}}} \def\proj{\mathbf{proj}} \def\R{\mathbb R} \def\Re{\mathbb R} \def\Rn{\R^n} \def\rank{\mathbf{rank}} \def\range{{\mathbf{range}}} \def\sign{{\mathbf{sign}}} \def\span{{\mathbf{span}}} \def\st{\hbox{\rm subject to}} \def\T{^\intercal} \def\textt#1{\quad\text{#1}\quad} \def\trace{\mathbf{trace}} \]

The singular value decomposition (SVD) reveals many of the most important properties of a matrix. It generalizes the eigenvalue decomposition to non-square matrices.

• geometric interpretation
• reduced SVD
• full SVD
• formal definition

Matrix Rank

The rank of a matrix \(A\) is the maximum number of linearly independent columns (or rows) of \(A\). It indicates the dimension of the subspace spanned by its columns (or rows).

• Column rank is the dimension of the column space \(\range(A)\)
• Row rank is the dimension of the row space \(\range(A^T)\)
• Full rank if \(\rank(A) = \min(m,n)\)
• for any matrix, the row and column rank are equal, so we just say rank

Example

\[ A = \begin{bmatrix} 1 & 2 & 3\\ 2 & 4 & 6\\ 3 & 6 & 9 \end{bmatrix} \]

Implications

• higher rank means more linearly independent vectors \(\Rightarrow\) more information or dimensions represented by the matrix
• for a square matrix, rank is the number of non-zero eigenvalues

Multiplication Table is Rank 1

 

u = collect(1:12)
A = u*u'

 

 

12×12 Matrix{Int64}:
  1   2   3   4   5   6   7   8    9   10   11   12
  2   4   6   8  10  12  14  16   18   20   22   24
  3   6   9  12  15  18  21  24   27   30   33   36
  4   8  12  16  20  24  28  32   36   40   44   48
  5  10  15  20  25  30  35  40   45   50   55   60
  6  12  18  24  30  36  42  48   54   60   66   72
  7  14  21  28  35  42  49  56   63   70   77   84
  8  16  24  32  40  48  56  64   72   80   88   96
  9  18  27  36  45  54  63  72   81   90   99  108
 10  20  30  40  50  60  70  80   90  100  110  120
 11  22  33  44  55  66  77  88   99  110  121  132
 12  24  36  48  60  72  84  96  108  120  132  144

 

Low-rank image approximation

Singular value decomposition

For any \(m\times n\) matrix \(A\) with rank \(r\) \[ \begin{aligned} A = U\Sigma V^T = [u_1\ |\ u_2\ |\cdots\ |\ u_r] \begin{bmatrix} \sigma_1 & & & \\ & \sigma_2 & & \\ & & \ddots & \\ & & & \sigma_r \\ \end{bmatrix} \begin{bmatrix} v_1^T \\ \hline v_2^T \\ \hline \vdots \\ \hline v_r^T \end{bmatrix} = \sum_{j=1}^r \sigma_j u_j v_j^T \end{aligned} \] left \(U\) and right \(V\) singular vectors are orthonormal and singular values: \[ U^T U = I_r, \qquad V^T V = I_r, \qquad \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0 \]

for \(j=1,\ldots,r\) \[ \begin{aligned} AV &= U\Sigma\\ Av_j &= \sigma_j u_j \end{aligned} \]

  \[ \begin{aligned} A^T U &= V\Sigma\\ A^T u_j &= \sigma_j v_j \end{aligned} \]

SVD Visualization

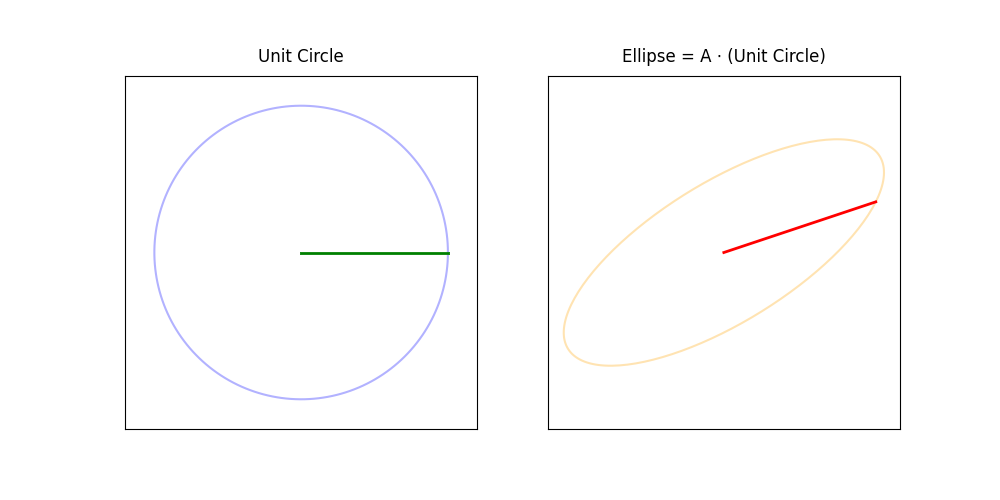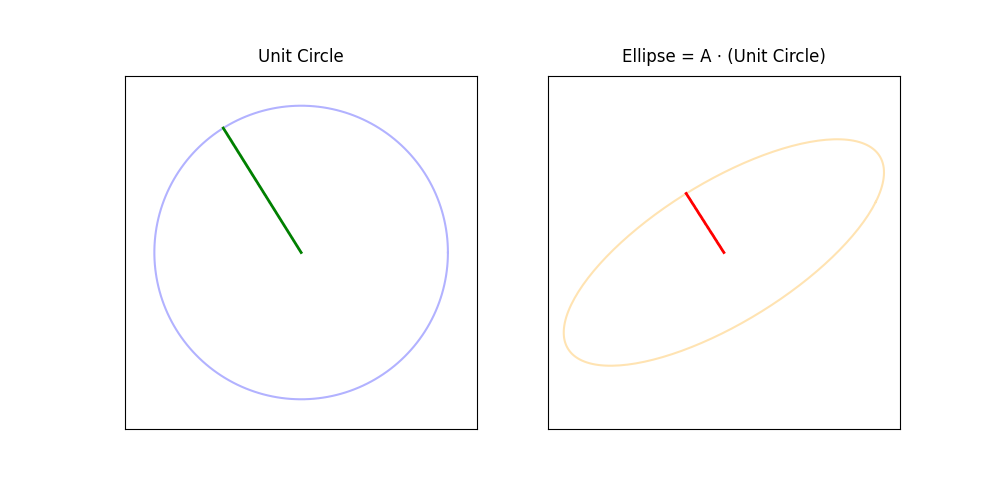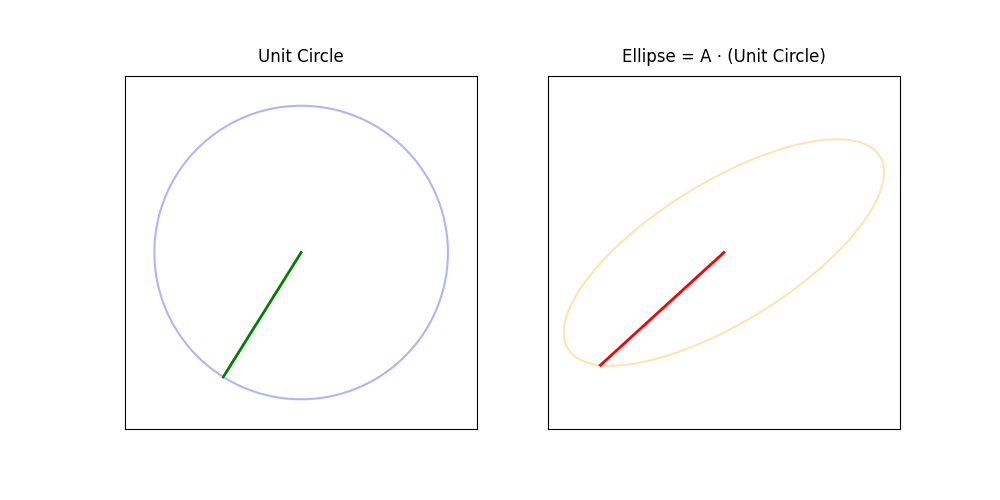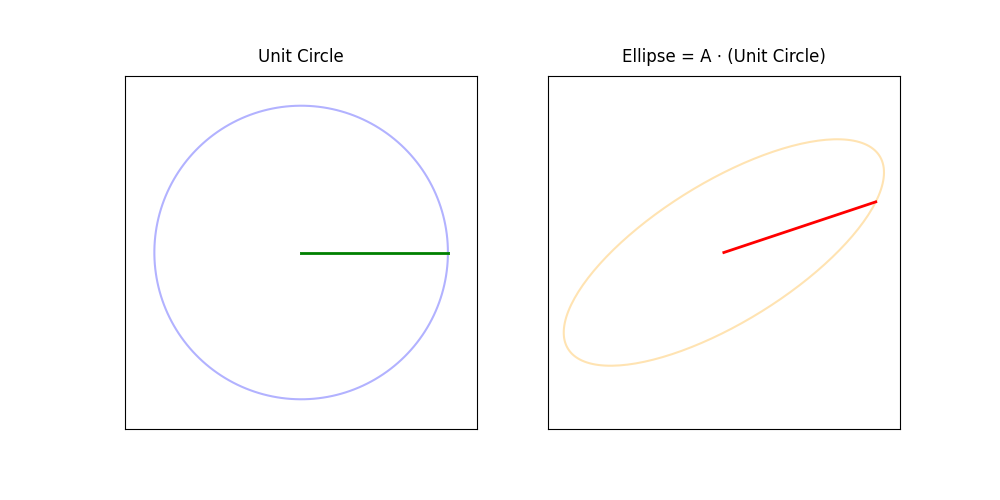
Question: Flag rank

What is the rank of the Finnish flag?

1. 1
2. 2
3. 3
4. 4
5. 5

Question: Flag rank II

What is the rank of the Greek flag?

1. 1
2. 2
3. 3
4. 4
5. 5

Column and Row Bases

The left- and right- singular vectors constitute orthogonal bases for the four fundamental subspaces of \(A\)

\[ \begin{aligned} \proj_{\range(A^T)} &= VV^T\\ \proj_{\Null(A)} &= I_n-VV^T \end{aligned} \]

\[ \begin{aligned} \proj_{\range(A)} &= UU^T\\ \proj_{\Null(A^T)} &= I_m-UU^T \end{aligned} \]

SVD Construction

Conceptually, we can construct the SVD from the Grammian \(A^T A\):

1. gather the eigenvalues of \(A^T A\) in descending order (may be multiplicity): \[ \lambda_1\geq \lambda_2\geq \cdots \geq \lambda_r > 0, \qquad \Lambda := \mathbf{Diag}(\lambda_1,\ldots,\lambda_r) \]

2. because \(A^T A\) is symmetric, the spectral theorem ensures it’s diagonalizable \[ A^T A = V\Lambda V^T \]

3. define singular values: \[ \sigma_i:=\sqrt{\lambda_i}, \qquad \Sigma:= \mathbf{Diag}(\sigma_1,\ldots,\sigma_r) \]

4. define left singular vectors (deduce that \(U\) is orthonormal): \[U:= AV\Sigma^{-1}\]

5. summary: \[A = U\Sigma V^T\]

Properties

Given SVD \(A = U\Sigma V^T\) with singular values \(\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0\)

1. \(U\) is a basis for \(\range(A)\)

2. \(V\) is a basis for \(\range(A^T)\)

3. spectral norm of \(A\): \[ \|A\|_2 = \max_{\|x\|_2=1} \|Ax\|_2 = \sigma_1 \]

4. Frobenious norm of \(A\): \[ \|A\|_F := \sqrt{\sum_{i=1}^m\sum_{j=1}^n a^2_{ij}} \equiv \sqrt{\trace(A^T A)}= \sqrt{\sum_{i=1}^r \sigma_i^2} \]

Question: Spectral norm I

Suppose that \(u\in\R^m\) and \(v\in\R^n\) are unit-norm vectors. Then the outer product \(uv^T\) is an \(m\times n\) matrix with rank 1. What is the spectral norm of \(uv^T\)?

1. \(\quad 1\)
2. \(\quad u^T v\)
3. \(\quad 2\)
4. \(\quad \|u\|_2 + \|v\|_2\)

Question: Spectral norm II

Suppose that \(x\in\R^m\) and \(y\in\R^n\) are nonzero vectors. Then the outer product \(xy^T\) is an \(m\times n\) matrix with rank 1. What is the spectral norm of \(xy^T\)?

1. \(\quad 1\)
2. \(\quad x^T y\)
3. \(\quad \|x\|_2\cdot \|y\|_2\)
4. \(\quad \|x\|_2 + \|y\|_2\)

Low-rank approximation

The SVD decomposes any matrix \(A\) with rank \(r\) into a sum of rank-1 matrices: \[ \begin{aligned} A = U\Sigma V^T = [u_1\ |\ u_2\ |\cdots\ |\ u_r] \begin{bmatrix} \sigma_1 & & & \\ & \sigma_2 & & \\ & & \ddots & \\ & & & \sigma_r \\ \end{bmatrix} \begin{bmatrix} v_1^T \\ \hline v_2^T \\ \hline \vdots \\ \hline v_r^T \end{bmatrix} % &= [\sigma_1u_1\ |\ \sigma_2u_2\ |\cdots\ |\ \sigma_ru_r] % \begin{bmatrix} % v_1^T \\ \hline v_2^T \\ \hline \vdots \\ \hline v_r^T % \end{bmatrix} \\ &= \sum_{j=1}^r \sigma_j u_j v_j^T \end{aligned} \]

Eckart-Young Theorem

The best rank-\(k\) approximation to \(A\) is given by rank-\(k\) approximation \[ A_k = \sum_{j=1}^k \sigma_j u_j v_j^T \] with error \(E_k := A - A_k\) satisfying \[ \|E_k\|_2 = \sigma_{k+1} \textt{and} \|E_k\|_F = \sqrt{\sum_{j=k+1}^r \sigma_j^2} \]

Full SVD

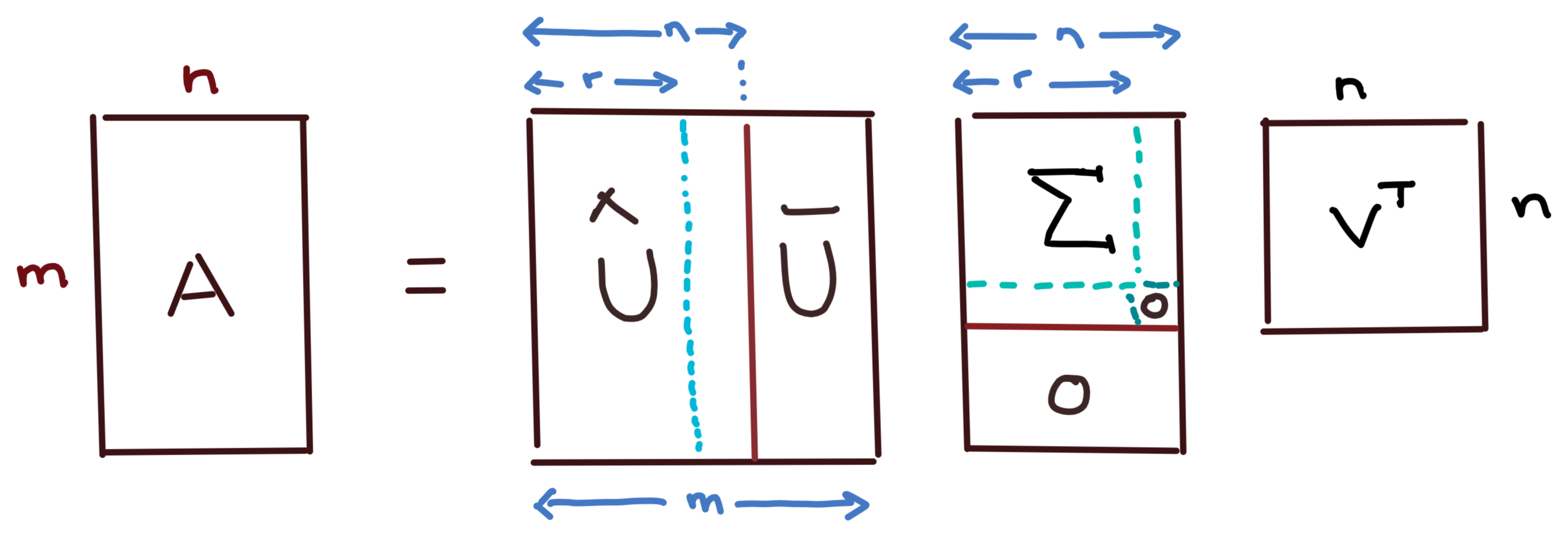
\[ \begin{aligned} U &= [\,\hat U \mid \bar U\, ]\\ \hat U &= [\, u_1,\ldots,u_r, u_{r+1}, \ldots, u_n\, ]\\ \bar U &= [\, u_{n+1}, \ldots, u_m\, ]\\ V &= [\, v_1,\ldots,v_n\, ]\\ \Sigma &= \Diag(\sigma_1,\ldots,\sigma_r,0,\ldots,0) \end{aligned} \]

Provides orthogonal bases for all four fundamental subspaces

\[ \begin{aligned} \range(A)&=\span\{u_1,\ldots,u_r\}\\ \Null(A^T)&=\span\{u_{r+1},\ldots,u_m\}\\ \range(A^T)&=\span\{v_1,\ldots,v_r\}\\ \Null(A)&=\span\{v_{r+1},\ldots,v_n\} \end{aligned} \]

Minimum norm least-squares solution

If \(A\) is \(m\times n\) with \(\rank(A)=r<n\), then infinitely many least-squares solutions: \[ \mathcal X = \{x\in\Rn \mid A^T A x = A^T b\} \]

SVD provides the minimum norm solution \(\bar x = \min\{ \|x\| \mid x\in\mathcal X\}\)

If \(A=U\Sigma V^T\) is the full SVD of \(A\), then \[ \begin{aligned} \|Ax-b\|^2 &= \|(U^T A V)(V^T x) - U^T b\|^2 \\ &= \|\Sigma y - U^T b\|^2 & (y:= V^T x)\\ &= \sum_{j=1}^r (\sigma_j y_j - \bar b_j)^2 + \sum_{j=r+1}^n \bar b_j^2 & (\bar b_j=u_j^T b)\\ \end{aligned} \] Choose \[ y_j = \begin{cases} \bar b_j/\sigma_j & j=1:r\\ 0 & j=r+1:n \end{cases} \quad\Longrightarrow\quad \bar x = V y = \sum_{j=1}^r \frac{u_j^T b}{\sigma_j} v_j \]

Pseudoinverse of a Matrix

The pseudoinverse of a matrix \(A\), denoted \(A^+\), generalizes the inverse for matrices that may not be square or full rank. If \(A = U \Sigma V^T\) is the SVD of \(A\), then: \[ A^+ := V \Sigma^+ U^T \quad\text{where}\quad \Sigma^+_{ij} = \begin{cases} 1 / \sigma_i & \text{if } \sigma_i > 0 \\ 0 & \text{if } \sigma_i = 0 \end{cases} \]

Key Properties

1. \(A^+ A\) projects onto the column space of \(A\)
2. \(A A^+\) projects onto the row space of \(A^T\)
3. \(A^+\) always exists for any matrix \(A\), regardless of its shape or rank

Connection to the Minimum Norm Solution

The pseudoinverse provides the minimum norm least-squares solution to \(\|A x - b\|\): \[ \bar{x} = A^+ b \]