Regularized Least Squares

The Pareto frontier

The standard least-squares problem can be interpreted as a method for recovering some underlying object (say, a signal or image) encoded in the vector $x_0$ using noisy measurements of the form

where $w$ is random noise and the matrix $A$ describes the measurement process. The least-squares problem

seeks a solution $x$ under the implicit assumption that the noise term $w_1$ is small.

But what if $x$ also needs to satisfy some other competing objective? Suppose, for example, that we have also available other set of measurements of $x_0$ of the form $d = Cx_0+w_2$, where $w_2$ is also random noise. The "best" choice for $x$ is not necessarily (1), and instead we wish to choose $x$ to balance the two objective values

Generally, we can make $f_1(x)$ or $f_2(x)$ small, but not both. The figure below sketches the relationship between the pair $\{f_1(x), f_2(x)\}$ for all values of $x$.

The objective pairs on the boundary of two regions is the Pareto frontier. We can compute these Pareto optimal solutions $x$ by minimizing the weighted sum objective

where the positive parameter $\lambda$ provides the relative weight between the objectives.

For fixed scalars $λ$ and $α$, the set

forms the graph of a line with slope of $-\lambda$. We may visualize the optimization problem (2) as the problem of finding the smallest value $\alpha$ such that the line is tangent to the Pareto frontier.

Tikhonov regularization

A particularly common example of regularized least-squares is Tikhonov, which has the form

for which the objective can be expressed as

If $D$ has full column rank, then the stacked matrix

necessarily also has full rank for any positive $\lambda$, which implies that the regularized problem always has a well-defined unique solution.

Example: Signal denoising

using LinearAlgebra
using Plots

Consider a noisy measurement

of a signal $x^\natural$, where the vector $w$ represents unknown noise. Here's a simple 1-dimensional noisy signal:

n = 300
t = LinRange(0, 4, n)
x = @. sin(t) + t*cos(t)^2
w = 0.1*randn(n)
b = x + w
plot(b, leg=:topleft, label="noisy signal")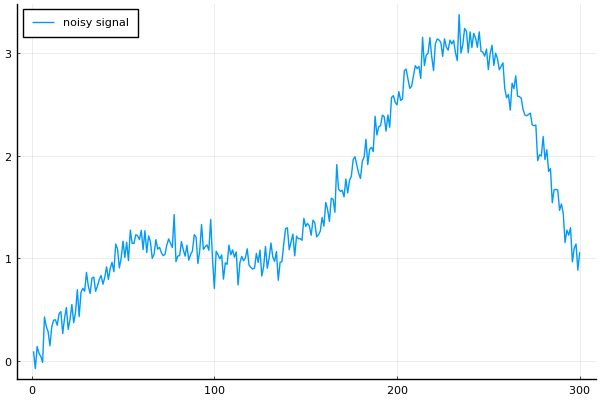

The obvious least-squares problem

isn't useful because the optimal solution is simply the noisy measurements $b$, and so it doesn't yield any new information. But suppose we believe that the signal is "smooth" in the sense that the consecutive elements of

change relatively little, i.e., the difference $|x_i-x_{i+1}|$ is small relative to $x$. In this case, we might balance the least-squares fit against the smoothness of the solution by instead solving the regularized least-squares problem

The role of the regularizer $f_2(x)$ is to promote smooth changes in the elements of $x$.

Matrix notation

We can alternatively write the above minimization program in matrix notation. Define the $(n-1)$-by-$n$ finite difference matrix

which when applied to a vector $x$, yields a vector of the differences:

Then we can rephrase the regularization objective as

This allows for a reformulation of the weighted leas squares objective into a familiar least squares objective:

So the solution to the weighted least squares minimization program (9) satisfies the normal equation $\hat{A}^T\!\hat{A}x = \hat{A}^T\!\hat{b}$, which simplifies to

The following function generates the required finite-difference matrix:

finiteDiff(n) = diagm(0 => ones(n), +1 => -ones(n-1))[1:n-1,:]

Here's an example of a small finite-difference matrix:

finiteDiff(4)

3×4 Matrix{Float64}:
 1.0  -1.0   0.0   0.0
 0.0   1.0  -1.0   0.0
 0.0   0.0   1.0  -1.0

The function below returns a generator, which produces $n$ logarithmically-spaced numbers in the interval $[x_1,x_2]$:

LogRange(x1, x2, n) = (10^y for y in range(log10(x1), log10(x2), length=n))

Now solve the regularized least-squares problem for several values of $\lambda\in[1,10^4]$:

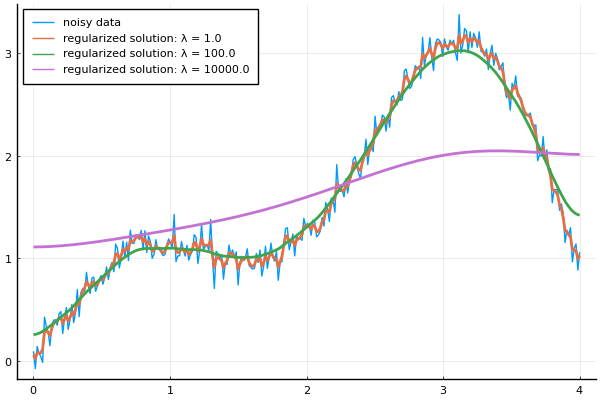
D = finiteDiff(n)
b̂ = [b; zeros(n-1)]
plot(t, b, w=1, leg =:topleft, label="noisy data")
for λ in LogRange(1e0, 1e4, 3) 
    Â = [ I; √λ*D ]
    xLS = Â \ b̂
    plot!(t, xLS, w=2, label="regularized solution: λ = $(λ)")
end

Note that the expression  = [ I; √λ*D ] contains the UniformScaling object, which represents an identity matrix of any size.